CSC 411: Artificial Intelligence

(Fall 2006)

Assignment 2: Chapters 3 and 4

Due by October 19, Thursday, 2006

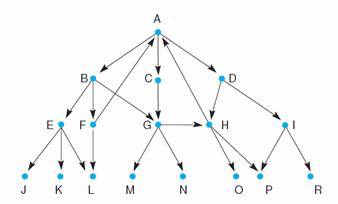
1. Carefully read and fully understand the backtrack algorithm (Page 97 of the textbook), and then “Hand run” the backtrack algorithm on the graph below. Begin from state A. Keep track of the successive values of NSL, SL, CS, etc.

2. Carefully read Section 3.2.3 and fully understand depth-first and breadth-first search to determine whether breadth-first search or depth-first search would be preferable for each of the following problems. Justify your answer.

a. A chess playing program

b. A medical diagnostic program

c. A program to determine the best sequence of manufacturing steps to go from raw materials to a finished product.

d. A program that attempts to determine if two expressions in the propositional calculus are equivalent.

3. Carefully read Section 3.2.1 and fully understand data-driven and goal-driven search to determine whether goal-driven or data-driven search would be preferable for solving each of the following problems. Justify you answer.

a. Diagnosing mechanical problems in an automobile.

b. A theorem prover for plane geometry

c. A program for examining sonar readings and interpreting them, e.g., telling a large submarine from a small submarine from a whale from a school of fish.

d. An expert system that will help a human classify plants by species, genus, etc.

4. The following figure is excerpted from Figure 4.3 of the textbook. Carefully read pages 123 through 126. Extend the “most wins” heuristic for tic-tac-toe plys deeper in the search space of the figure. What is the total number of states examined using this heuristics? Would the traditional hill-climbing algorithm work in this situation? Why?

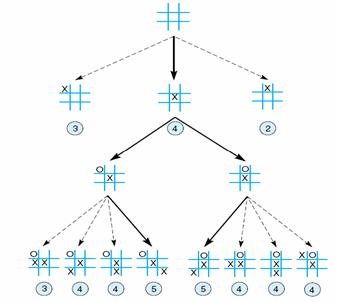
5. The sliding-tile puzzle consists of three black tiles, three white tiles, and an empty space in the configuration shown in the figure below. The puzzle has two legal moves with associated costs:

i. A tile may move into an adjacent empty location. This has a cost of 1.

ii. A tile can hop over one or two other tiles into the empty position. This has a cost equal to the number of tiles jumped over.

The goal is to have all the white tiles to the left of all the black tiles. The position of the blank is not important.

a. Analyze the state space with respect to complexity and looping.

b. Propose a heuristic for solving this problem and analyze it with respect to admissibility, monotonicity, and informedness.

6. Carefully read Section 4.4 and fully understand the Minimax procedure and the Alpha-Beta procedure. Consider the following figure.

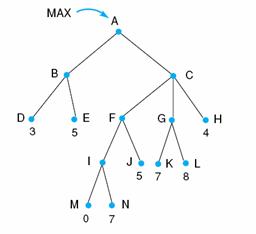
a. Perform minimax on the above tree.

b. Perform a left-to-right alpha-beta prune on the above tree.

c. Perform a right-to-left prune on the same tree.

d. Discuss why a different pruning occurs.