CSC 411: Artificial Intelligence

(Fall 2006)

Assignment 2: Chapters 3 and 4

Due by October 19, Thursday, 2006

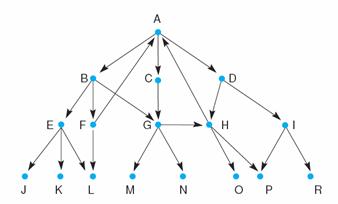
1. Carefully read and fully understand the backtrack algorithm (Page 97 of the textbook), and then “Hand run” the backtrack algorithm on the graph below. Begin from state A. Keep track of the successive values of NSL, SL, CS, etc.

Solution:

We assume there is no goal state in the search space. Initialize:

SL = [A], NSL = [A], DE=[], CS = A;

Loop CS SL NSL DE

0 A [A] [A] []

1 B [B A] [B C D A] []

2 E [E B A] [E F G B C D A] []

3 J [J E B A] [J K L E F G B C D A] []

4 K [K E B A] [K L E F G B C D A] [J]

5 L [L E B A] [L E F G B C D A] [K J]

6 F [F B A] [F G B C D A] [E L K J]

7 G [G B A] [G B C D A] [F E L K J]

8 M [M G B A] [M N H G B C D A] [F E L K J]

9 N [N G B A] [N H G B C D A] [M F E L K J]

10 H [H G B A] [H G B C D A] [N M F E L K J]

11 O [O H G B A] [O P H G B C D A] [N M F E L K J]

12 P [P H G B A] [M N H G B C D A] [O N M F E L K J]

13 C [C A] [C D A] [G H P O N M F E L K J]

14 D [D A] [D A] [C G H P O N M F E L K J]

15 I [I D A] [I D A] [C G H P O N M F E L K J]

16 R [R I D A] [R I D A] [C G H P O N M F E L K J]

17 - [] [] [A D I R C G H P O N M F E L K J]

The algorithm returns FAIL.

2. Carefully read Section 3.2.3 and fully understand depth-first and breadth-first search to determine whether breadth-first search or depth-first search would be preferable for each of the following problems. Justify your answer.

a. A chess playing program

b. A medical diagnostic program

c. A program to determine the best sequence of manufacturing steps to go from raw materials to a finished product.

d. A program that attempts to determine if two expressions in the propositional calculus are equivalent.

Solution:

a. Has to be depth-first, or at least guided (with heuristics) depth-first (n-ply depth). The branching factor is too large in chess to get to an interesting depth with exhaustive breadth-first search.

b. Usually done depth-first. This allows the program to follow a line of reasoning and only change to a new goal or hypothesis when a previous one is confirmed or denied.

c. It should at least have a flavor of breadth-first, if not be totally breadth-first so that some process aren’t satisfied to the detriment of later ones.

d. Usually depth-first, as was the Unify algorithm in Chapter 2. This allows unification substitutions to be pushed forward through the remaining expression.

3. Carefully read Section 3.2.1 and fully understand data-driven and goal-driven search to determine whether goal-driven or data-driven search would be preferable for solving each of the following problems. Justify you answer.

a. Diagnosing mechanical problems in an automobile.

b. A theorem prover for plane geometry

c. A program for examining sonar readings and interpreting them, e.g., telling a large submarine from a small submarine from a whale from a school of fish.

d. An expert system that will help a human classify plants by species, genus, etc.

Solution:

a. Usually goal-driven. The search can be where the data is collected, suggesting possible goals (causes of the symptoms). Then each goal is checked.

b. Theorem provers are almost universally goal-driven. The alternative of developing all possible theorems that follow from the axioms of geometry hoping to find the theorem in question is both theoretically and computationally impossible for any interesting proof.

c. This type of problem is almost always data-driven, unless there are very few goals to investigate.

d. Usually data-driven. There are too many possible goals in most interesting cases.

4. The following figure is excerpted from Figure 4.3 of the textbook. Carefully read pages 123 through 126. Extend the “most wins” heuristic for tic-tac-toe plys deeper in the search space of the figure. What is the total number of states examined using this heuristics? Would the traditional hill-climbing algorithm work in this situation? Why?

Solution:

To simplify things we will add two simple heuristics to the state evaluation.

o Take a direct win or a “forking” win when possible. A “fork” move produces two possible next move victories where the opponent can only stop one of them.

o Always select a move that avoids a direct loss.

In this case the opponent will have only three possible responses to your selection in the left-most subtree. Each of these has only one response. In the right-most subtree, your opponent has six possible responses, but must select the one that avoids a direct loss. In this situation your next move is a “forking’ win. Thus there are only four next states for your opponent to consider and each of these have a direct required response for a total of eight next-states to be considered to go two levels deeper in the search space. Only one of your opponent’s four choices will avoid a sure loss. This is in the left subtree.

Yes, hill climbing works here. In fact the example given is an instance of hill climbing. In games where backing out of an already selected move in usually not possible, a form of hill climbing is often appropriate.

5. The sliding-tile puzzle consists of three black tiles, three white tiles, and an empty space in the configuration shown in the figure below. The puzzle has two legal moves with associated costs:

i. A tile may move into an adjacent empty location. This has a cost of 1.

ii. A tile can hop over one or two other tiles into the empty position. This has a cost equal to the number of tiles jumped over.

The goal is to have all the white tiles to the left of all the black tiles. The position of the blank is not important.

a. Analyze the state space with respect to complexity and looping.

b. Propose a heuristic for solving this problem and analyze it with respect to admissibility, monotonicity, and informedness.

Solution:

This is an excellent problem to help understand the use of heuristics and the properties of Section 4.3. Breadth-first search is of course admissible, monotonic, and very uninformed. Counting tiles out of the goal position is a simple useful heuristic that is admissible. A form of this heuristic would be to count all white tiles on the wrong side of each black tile. Counting tiles out of place is not monotonic, but is more informed than breadth-first search. An easy way to prove that a heuristic is non-monotonic is to watch its value change as it goes along a search path. Other versions of this problem either limit the kinds of jumps possible or change the cost of jumps.

6. Carefully read Section 4.4 and fully understand the Minimax procedure and the Alpha-Beta procedure. Consider the following figure.

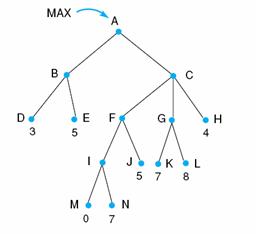
a. Perform minimax on the above tree.

b. Perform a left-to-right alpha-beta prune on the above tree.

c. Perform a right-to-left prune on the same tree.

d. Discuss why a different pruning occurs.

Solution:

a. Node’s score as following: I – 0, F – 5, G – 8, B – 3, C – 4, A – 4.

b. Left-to-right alpha-beta: (I, N) and (G, L) will be cut.

MIN on left-most deepest subtree (3, 5) to get α at A=3.

From next left-most deepest subtree (M, N), MIN of 0, prune.

F is now 5 and β at C = 5.

Subtree(K, L) is MAX, so with 7 of K, L is β pruned.

Seeing the right-most 4, β at C=4, and α at A=4, the final backed up value.

c. Right-to-left alpha-beta:(G,K) and (F, I) will be cut.

Starting at the right-most deepest subtree, H gives β of C=4.

Seeing 8 at L in subtree (K, L), K with 7 is β pruned.

Seeing 5 at J next, the entire subtree(M, N) is β pruned.

A takes on the α value of 4.

5 and then 3 are examined (MIN) in the left-most subtree. The final value of A is 4.

d. Because the nodes in the tree are examined in different orders.