CSC 461: Computer Graphics I (Fall 2006)

Sample Solution to Assignment 2 (Chapters 2 and 3)

1. We saw that a fundamental operation in graphics system is to map a point (x, y), which lies within a clipping rectangle, to a point (x_s, y_s), which lies in the viewport of a window on the screen. Assume that the two rectangles are defined by  OpenGL function calls

glViewport(u, v, w, h);

gluOrtho2D(x_min, x_max, y_min, y_max);

Find the mathematical equations that map (x, y) into (x_s, y_s).

Solution: We can solve this problem separately in the x and y directions. The transformation is linear, that is x_s=ax+b, y_s=cy+d. We must maintain proportions, so that x_s in the same relative position in the viewport as x is in the window. Hence

, . Likewise, .

2. Devise a test for the convexity of a two-dimensional polygon. (You should describe your test algorithm in either pseudo code or natural languages considering different cases)

Solution: Consider the lines defined by the sides of the polygon. We can assign a direction for each of these lines by traversing the vertices in a counter-clockwise order. One very simple test is obtained by noting that any point inside the object is on the left of each of these lines. Thus, if we substitute the point into the equation for each of the lines (ax+by+c), we should always get the same sign. Thus, we have the following algorithm:

For each side of the polygon

Assume the line equation ax+by+c

For each vertex of the polygon (x₀,y₀)

Find the sign of ax₀+by₀+c

If the equations have the different sign, return false – no convex

Return true – convex polygon

3. The mapping from a point in object or world coordinates to one in screen coordinates is well defined. It is not invertible because we go from three dimensions to two dimensions. Suppose, however, that we are working with a two-dimensional application. Is the mapping invertible? What problem can arise if you use a two-dimensional mapping to return to a position in object or world coordinates by a locator device.

Solution: No, it is still not invertible. There are a couple of potential problems.

o One is that the application program can map different points in user coordinates to the same point in screen coordinates.

o Second, a given position on the screen when transformed back into user coordinates may lie outside the user window,

4. Consider a table with a two-dimensional sensing device located at the end of two linked arms, as shown in the figure. Suppose that the lengths of the two arms are fixed, and the arms are connected by simple (1-degree-of-freedom) pivot joints. Determine the relationship between the joint angles θ and φ and the position of the sensor (located at the end of the second arm).

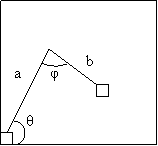
Solution: Let (x₁, y₁) be the joint of the two arms, and (x₂, y₂) the end of the second arm. Assuming the lower-left corner is the origin. Then

x₁ = acosθ, y₁ = asinθ

Similarly, using the angle φ, we can find

x₂ = x₁ + bcos(π-θ-φ), and y₂=y₁- bsin(π-θ-φ).