CSC 461: Computer Graphics I (Fall 2006)
Sample Solution to Written Assignment 3 (Chapter 4)
Due
In Chapter 4, geometric objects and transformations are introduced, focusing on linear vector space, affine space, coordinate systems and frames, transformations between coordinate systems, homogeneous coordinates. Also, four transformations, including translation, rotation, scaling, and shear, are discussed theoretically and how they are implemented in OpenGL. In this assignment, you should read the text and course notes (Powerpoint) to fully understand these topics, and solve the following questions.
1. Show that the following sequences commute:
o A rotation and a uniform scaling
o Two rotations about the same axis
o Two translations
Solution:
1) Let R be the rotation matrix and S be the uniform
scaling matrix, we have
RS = RS(a,
a, a)
= aR = SR
2) Let Rx be the rotation matrix of rotations about X-axis.
If we multiply and use the standard trigonometric identities for the sine and
cosine of the sum of two angles, we find
Rx(q)Rx(f) = Rx(q+f ) =
Rx(f)Rx(q)
3) Let T be the translation matrix. By simply multiplying the matrices
we find
T(x1,
y1, z1)T(x2, y2, z2) =
T(x1+x2, y1+y2, z1+z2)
= T(x2, y2, z2)T(x1, y1,
z1)
2. If we are interested in only two-dimensional graphics, we can use three-dimensional homogeneous coordinates by representing a point as p=[x y 1]T and a vector as v=[a b 0]T. Find the 3 ´ 3 rotation, translation, scaling, and shear matrices. How many degrees of freedom are there in an affine transformation for transforming two-dimensional points?
Solution: Translation: T=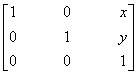
Rotation: R
= 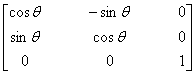
Scaling: S
= 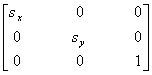
Shear: H
= 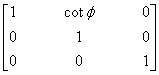
3. We have used vertices in three dimensions to define objects such as three-dimensional polygons. Given a set of vertices, find a test to determine whether the polygon that they determine is planar.
Solution: One test is to use the first three vertices to find the equation of the plane ax + by + cz + d = 0. Although there are four coefficients in the equation only three are independent so we can select one arbitrarily or normalize so that a2 + b2 + c2 = 1. Then we can successively evaluate ax + by + cz + d for the other vertices. A vertex will be on the plane if we evaluate to zero. An equivalent test is to form the matrix
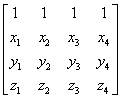
for each i = 4, … If the determinant of this
matrix is zero the i-th vertex is in the plane
determined by the first three.
4. Given two non-parallel three dimensional vectors u and v, how can we form an orthogonal coordinate system in which u is one of the basis vectors?
Solution: The vector a = u × v is orthogonal
to u and v. The vector u × a is orthogonal to u and a.
Hence, u, a, and b form an orthogonal coordinate system.