CSC 311: Data Structures
(Fall 2007)
Assignment 3: Chapters 8 through 9
All questions are equally scored.
1. Priority Queue
a. Adaptor design pattern: Show how to implement the stack ADT using only a priority queue and one additional integer instance variable.
Solution: Maintain a variable m initialized to 0. On
a push operation for element 2, call insert(m, e) and decrement m. On a pop operation, call removeMin.
b. Algorithm design: Describe in detail an implementation of a priority queue based on a sorted array. Show that this implementation achieves O(1) time for operations min and removeMin and O(n) time for operation insert.
Solution:
Maintain a counter to keep the
number of elements in the sorted array. On an insertion operation, start from
the first element until find an element e
that is less than the element to be inserted. If no e exists, the new element
is inserted at the index of the counter, otherwise all elements after e
(including e) are shifted right and the new element is inserted at the index of
e. The counter is increased by 1. This takes time of O(n).
On a removal operation, the last element at the index of the counter, is
removed and the counter is decreased by 1, which takes time of O(1).
2. Heap-sort
a. Illustrate the execution of the heap-sort algorithm on the following input sequence: 2, 5, 16, 4, 10, 23, 39, 18, 26, 15.
Solution: First step to
insert the input sequence into an initially empty heap, shown as below:
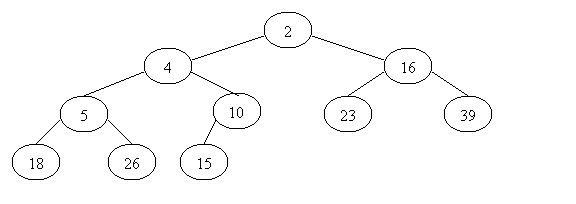
Second
step to remove the root until the heap is empty.
b. Show that the sum Sni=1logi, which appears in the analysis of heap-sort,, is W(nlogn).
Solution: Sni=1logi = log(Πni=1i)=log(n!). (n/2)(n/2) ≤ n! ≤ (n)(n/2).
3. Map and Search Table
a. Describe how to use a map to implement the dictionary ADT, assuming that the user may attempt to insert entries with the same key.
Solution: The elements in
the map should be a collection (such as a set)
1) isEmpty – same as map
2) size – call
entries() to get all entries, each of which is a collection; sum the size of
all these collections
3) find(k) – get(k)
and then arbitrarily select one
4) findAll(k) – get(k).iterator()
5) insert(k, v) –
put(k, insert v to put(k, v))
6) remove(e) –
collection ß get(k); collection.remove( e.value()); put(e.key(),
collection)
7) entries() – iteratorßentries();
for each element in the iterator e, for each element
c in e.value(),
iterate entries <e.key(), c>
b. Design a variation of binary search for performing operation findAll(k) in a dictionary implemented with an ordered search table, and show that it runs in time O(logn + s), where n is the number of elements in the dictionary and s is the size of the iterator returned.
Solution: Consider a sorted array as the ordered
search table. findAll(k) uses binary search to find ONE k in the sorted array.
This takes time of O(logn).
All other k’s must be
adjacent to this k. Simply probe forward and backward to find all other k’s. This takes time of O(s).
4. Hash Table: Draw the 11-entry hash table that results from using the hash function, h(i)=(2i+5) mode 11, to hash the ksys 12, 44, 13, 88, 23, 94, 11, 39, 20, 16, and 5, assuming collisions are handled by
a. chaining;
Solution:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Keys |
|
20 |
|
|
16 |
44 |
94 |
12 |
|
13 |
|
|
|
|
|
|
|
5 |
88 |
39 |
23 |
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
b. linear probing;
Solution:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Keys |
11 |
39 |
20 |
5 |
16 |
44 |
88 |
12 |
23 |
13 |
94 |
c. quadratic probing, up to the point where the method fails;
Solution:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Keys |
- |
20 |
16 |
11 |
39 |
44 |
88 |
12 |
23 |
13 |
94 |
d. double hashing using the secondary hash function h’(k) = 7 – (k mod 7).
Solution:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Keys |
23 |
20 |
88 |
39 |
16 |
44 |
94 |
12 |
5 |
13 |
11 |