CSC311 Midterm Examination 2

(Fall 2006)

1. Priority Queues and Heaps (20 points):

a. (4 points) List methods of priority queues.

b. (8 points) Illustrate the heap after inserting the following input sequence: 5, 16, 4, 10, 26, 2, 39, 15, 18, 23 to an empty heap, and then the heap after removing the minimum.

c. (8 points) Briefly explain the Priority Queue Sort algorithm, and analyze the time complexity of the algorithm when the priority queue is implemented with a sorted list, an unsorted list, and a heap, respectively.

2. Hash table. (15 points, 5 points each)

a. What is the worst-case time for putting n entries in an initially empty hash table, with collisions resolved by chaining? What is the best case? What is the average case?

b. Given the following sequence of keys: 6, 4, 8, 26, 12, 15, 5.

i. Draw the 7-entry hash table that results from using the hash function h(i) = (3i+1) mod 7, to hash the above keys, assuming collisions are resolved by chaining.

ii. What is the result of above question when collisions are handled by double hashing using the secondary has function h’(k) = 7 – (k mod 7)?

3. Search Trees (35 points): Given the sequence of keys: 1, 2, 3, 4, 10, 6, 5, 9, 8, 7.

a. Binary search tree: (10 points)

i. Insert this sequence of keys into an empty binary search tree. Draw the tree.

ii. Delete the keys 4 and 5 from above binary search tree. Draw the tree after each deletion.

b. AVL Tree: (10 points)

i. Insert this sequence of keys into an empty AVL tree. Draw the tree.

ii. Delete the keys 4 and 5 from above AVL tree. Draw the tree after each deletion.

c. (2-4) Tree and Red-back Tree: (15 points)

i. Insert the given sequence of keys into an empty (2-4) search tree. Draw the tree.

ii. Delete the keys 4 and 5 from above (2-4) search tree. Draw the tree after each deletion.

iii. Convert the above (2-4) tree to a red-black tree

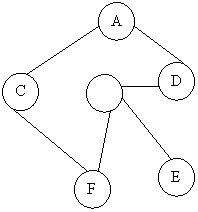
4. Graphs (10 points): The following is an undirected graph.  

1) Give the DFS result starting at vertex A

2) Give the BFS result starting at vertex A