Tour 5: Introducing Transformations
Up until now, we've focused on the compass-and-straightedge-derived commands in the Construct menu for doing our geometry. In this tour, you'll explore the Transform menu commands, based in transformational geometry, and ultimately tile the plane with parallelograms.
What You Will Learn
How to reflect figures across marked mirrors
How to translate figures by marked vectors
How to use the Merge command to alter the geometric properties of figures in a sketch
Reflections of a Triangle
In which you use Sketchpad to explore the other side of the looking glass . . .
In a new sketch, use the Segment tool to draw a triangle on the left side of the sketch window.
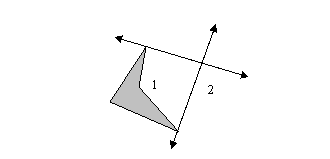
Draw a vertical segment in the middle of your screen. Holding down the Shift key while you draw helps keep the segment vertical (though it can still be dragged any which way later on).
While this segment is still selected, choose Mark Mirror from the Transform menu. A brief animation indicates that the segment has been marked as a mirror.
Select the whole triangle using a Selection Rectangle.
With your triangle selected, choose Reflect from the Transform menu. A mirror image of your triangle should appear on the other side of your "mirror" segment.
Alter your original triangle. What happens to the mirror image? Move your triangle around, make it bigger, smaller, move it closer to the mirror, further away, across. Try to predict the associated movements of the image triangle. What happens when you drag the image triangle? The mirror segment?
Draw a horizontal mirror and reflect both triangles across it. Explore and predict the motions of the three image triangles when you change your original triangle. Explore what happens when you change the relative positions of the two mirror segments and make them non-perpendicular.
Dynamic Translations
Add a new, blank page to your document.
Construct a general quadrilateral interior. To do this, choose the Point tool, then hold down the Shift key as you click in four different spots in the sketch window. With the four points selected, choose Quadrilateral Interior from the Construct menu.
Construct the four sides of your polygon. (A shortcut: Select the interior and choose Select Parents from the Edit menu. Now choose Segments from the Construct menu.)
Use the Segment tool to draw a segment in a blank area of the sketch plane. Show the labels of the two endpoints of the new segment, then select them. (Note the order of selection.)
Choose Mark Vector from the Transform menu. A brief animation from the first selected point to the second selected point indicates that the vector has been marked.
Select the sides and interior of your polygon. Choose Translate from the Transform menu. The Translate dialog box appears. Click Translate to translate by the marked vector.
Drag an endpoint of the segment defining the translation vector. What happens to the translated image?
Select the translated sides and interior and translate them again by the marked vector. (You won't need to mark the vector again -- just go straight to the Translate command.) Do this several times in a row to get several (five to eight) translated images.
Tiling Parallelograms
Add a duplicate of the current page to your document.
Drag point B so that the images are quite spread apart.
To turn your quadrilateral into
a parallelogram, you'll only have to "redefine" one of its vertices -- the
other
three will remain unchanged. Pick which three should remain as they are,
then construct a new point to be the fourth vertex of the
parallelogram. Hide everything new in this step but the point just
constructed.

Select the "other" quadrilateral vertex and the newly constructed point (points 1 and 2 in the figure at step 18) and choose Merge Points from the Edit menu. Use the Drag Test to confirm that your polygons are indeed parallelograms no matter what.
Parallelograms are special in that they tile the plane. In other words, they can be arranged in such a way that they fill the entire plane without overlaps or holes. You'll demonstrate this fact in the next section.
Drag objects until your sketch looks more or less like the figure below.
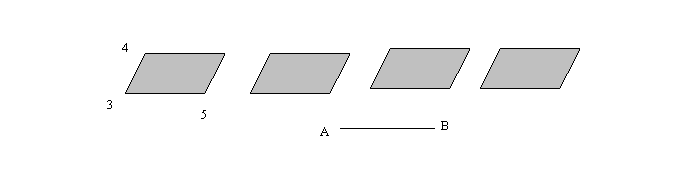
Mark a new vector from point 3 to point 4 (see the figure above).
Translate everything in the sketch (except line AB and its endpoints) by the marked vector. Repeat several (five to eight) more times.
Drag point B until your parallelograms indeed tile the plane. How many such locations are there for point B?
To fix your construction so that
the parallelograms always tile the plane, no matter what is dragged,
merge point A to point 3, then merge point B to point 5.
Further Challenges
Do all quadrilaterals tile the plane or just certain special ones? Use Sketchpad to explore this question.