Tour 6: A Sine
Wave Tracer
This tour introduces you to
Sketchpad animation as you work through an activity with The Geometer's
Sketchpad. In this exploration, you'll construct an animation "engine" that
traces out a special curve called a sine wave. Variations of sine curves are the
graphs of functions called periodic functions, functions that repeat themselves.
The motion of a pendulum and ocean tides are examples of periodic functions.
Sketch and
Investigate
-
Construct a horizontal segment
AB.

-
Construct a circle with center A
and radius endpoint C.
-
Construct point D on AB.
-
Construct a line perpendicular to AB through point D.
Select point D and AB; then, in the Construct menu, choose
Perpendicular Line.-
Construct point E on the circle.
-
Construct a line parallel to AB
through point E.
-
Construct point F, the point of
intersection of the vertical line through point D and the horizontal line
through point E.
Q1
Drag point D and describe what happens to point F.
Q2
Drag point E around the circle and describe what point
F does.
Q3
In a minute, you'll create an animation in your sketch
that combines these two motions. But first try to guess what the path of
point F will be when point D moves to the right along the segment at the
same time that point E is moving around the circle. Sketch the path you
imagine below.
-
Make an action button that
animates point D forward along AB and point E forward around the circle.
Select points D and E and choose Edit |Action Buttons
|Animation.
Choose forward in the Direction pop-up menu for point D.-
Move point D so that it's just
to the right of the circle.
-
Select point F; then, in the
Display menu, choose
Trace Intersection.
-
Press the
Animation button.
Q4
In the space below, sketch the path traced by point F.
Does the actual path resemble your guess in Q3? How is it different?
-
Select the circle; then, in the
Graph menu, choose Define
Unit Circle. You should get a graph with the origin at point A. Point
B should lie on the x-axis. The y-coordinate of point F above AB is the
value of the sine of <EAD.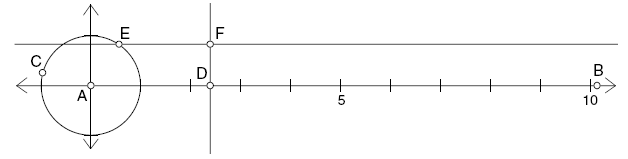
Q5
If the circle has a radius of 1 grid unit, what is its
circumference in grid units? (Calculate this yourself; don't use Sketchpad
to measure it because Sketchpad will measure in inches or centimeters, not
grid units.)
-
Measure the coordinates of point
B.
-
Adjust the segment and the
circle until you can make the curve trace back on itself instead of drawing
a new curve every time. (Keep point B on the x-axis.)
Q6
What's the relationship between the
x-coordinate of point B and the circumference of the circle (in grid units)?
Explain why you think this is so.
Extension:
"Special Points"
In the next section, you'll add the
right triangle associated with point E and also add a new type of button --
Movement buttons --
that will move point E to exact locations corresponding to angles of 30, 45, and
60 degrees.
-
Measure the coordinates of point
E.
-
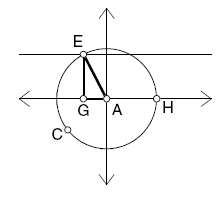
Construct the line through point
E, perpendicular to the x-axis.
- Construct the intersection point of this
new line and the x-axis. Label the point G
-
Construct the point at (1, 0) and label it H.
(You can either choose Plot Points from
the Graph menu or simply click on the spot to get the point of intersection.)
-
Measure <HAE.
-
Hide the perpendicular line and construct
segments from A to E, from G to E, and from
A to G. Make these three segments thick and
red. This is your "reference triangle."
Now you'll create points on the circle at 30, 45, and 60 degrees. You'll do this
by
rotating point H about the origin, or A.
-
Double-click point A. This marks it as a center of rotation.
-
Select point H and choose
Rotate from the Transform menu. Type 30 and
click Rotate.
-
Select point E and the new point in that order and choose
Movement from
the Edit | Action Buttons submenu. Leave the speed at medium. On the
Label panel, change the label of the button to
"30 degrees."
-
Hide the new point (at 30 degrees), then press your button. Point E should
gracefully move around the circle until <HAE is 30 degrees.
-
Repeat steps 22 and 23 for 45 and 60 degrees.
Further
Challenges


