|
|
|
Lecture Notes
Click here for the latest notes.
January 28, 2009
The meaning of "meta"
"Meta"
means "after" (in Greek). A selection of Aristotle's smaller writings
had been collected in one untitled chapter after his "Physics" by later
editors of his work. That chapter was referred to as "Metaphysics"
(literally: "after the Physics"). It contained subjects that we
classify today as metaphysics, or "beyond physics".
Then the
prefix "meta" in the similar meaning was transplanted to other branches
of philosophy and science, which gave rise to such terms as
"metamathematics", "metalogic", etc.
Today, "meta" usually refers
to something that is externous to a subject in question (or beyond it).
For instance, "metalanguage" means a (higher level) language in which
to express sentences about the language in question, "metatheory" means
a theory in metalanguage, "metasymbol" means a symbol of the metalanguage, etc.
The meaning of "context-free" and "context-sensitive"
"Context-free"
is a property of a syntactical object indicating that its meaning does
not depend on the context that is is used. For instance, a the meaning
of the sentence "For every x there exists y such that y is not equal x"
is context-free.
"Context-sensitive" refers to objects whose
meaning may depend on the context that is used. For instance, in this
inductive definition of a number:
0 is a number
If n is a number then the successor of n is a number
Nothing else is a number
the clause "nothing else is a number" is context sensitive.
"Context-free
grammar" is a grammar whose productions may be applied to any
occurrence of the non-terminal symbol on the left-hand side of the
production, regardless of the context of that occurrence.
Added after class:
A context-free grammar for the language PALINDROME (abbreviated as P)
defined
as the set of all binary strings that read the same forward and
backward (for instance 0110110 is in P while 111011 is not).
P --> e | 0 | 1 | 0P0 | 1P1
where e denotes the empty string.
It is relatively easy to find a derivation of 0110110 but it's more difficult to show that 111011 cannot be derived by the above grammar.
February 4, 2009
A variable in compile time (sometimes in runtime, too) is defined by an address to a block that has the following structure:
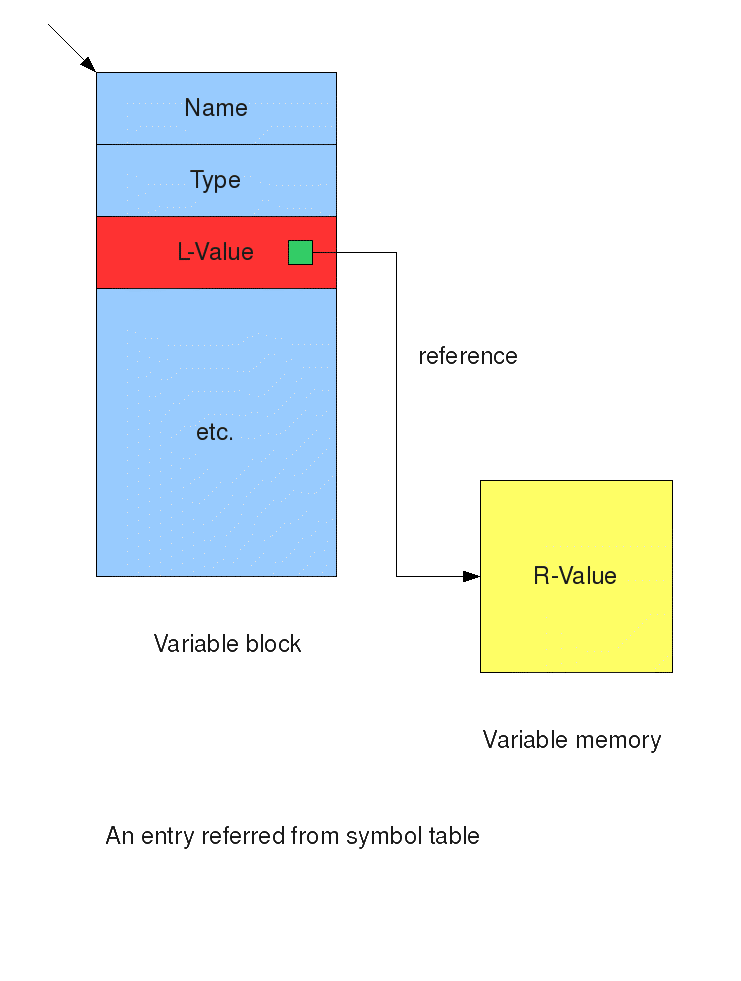
Some details of the above scheme (and in the comments below) may be depend on implementation.
Variable
block exists in compile time and may be totally or partially disposed
after the compilation is complete, except that the L-value will always
survive in some form in the executable code. Variable memory exists in
runtime.
The L-value serves as a reference to the R-value.
The L-value is typically used as the value for arrays and objects.
The R-value is typically used as the value for simple variables of basic types.
The
"L" and "R" in the above taxonomy comes from the fact that R-value must
be retrieved while evaluating a simple variable that occurs on the
Right-hand (hence "R") side of an assignment statement, while only the
L-value must be retrieved while assigning a new value to the target
variable that occurs on the Left-hand (hence "L") side of an assignment
statement.
(Notice that if one cannot retrieve the R-value without first retrieving the L-value.)
However, assigning a new value to a simple variable of basic type doesn't change its L-value, only R-value.
Assigning
a new value to an array or object does change its L-value while leaving the
R-value unchanged (unless the overwritten old L-value was the only
reference to that R-value in the program; in such a case, the variable
(array in this case) memory is being deallocated.
February 18, 2009
Clarification of inaccuracy in the text
The range for single-precision (32-bit) floating number (excluding "exceptional" values like +-infinity, NaN) is approximately:
<-1038, 1038>
The maximum accuracy is assumed around 0 (in the interval <-10-38, 10-38>) and is approximately equal to 10-45. In particular, the smallest positive number is approximately 10-45.
The range for double-precision (64-bit) floating number (excluding "exceptional" values like +-infinity, NaN) is approximately:
<-10308, 10308>
The maximum accuracy is assumed around 0 (in the interval <-10-308, 10-308>) and is approximately equal to 10-323. In particular, the smallest positive number is approximately 10-323.
For both representations, the value of binary representation is given by function f:
for e > 0: f(s, e, m, b) = (-1)s * 1.m * 2e-b (the so-called normalized form, just like in the textbook)
for e = 0: f(s, 0, m, b) = (-1)s * 0.m * 21-b (the so-called denormalized form, the missing part of the definition)
where
- s is the sign bit
- e is the exponent (an unsigned binary number)
- m is the mantissa (an unsigned binary number)
- b is the bias (b = 127 for 32-bit floating numbers and b = 1023 for 64-bit floating numbers)
(see Fig. 5.1 p 107 in the textbook).
In
particular, f(s, 0, 0, b) = 0, so both 10...0 and 00...0 represent the
value 0 (the former is a "negative" 0 and the latter is a "positive" 0).
The smallest positive number is represented by 00...01 and is given by f(0, 0, 1, b) = 2-23 * 2-126 = 10-45 for 32-bit floating numbers or 2-52 * 2-1022 = 10-323 for 64-bit floating numbers.
The largest negative number is represented by 10...01 and is given by f(1, 0, 1, b) = -2-23 * 2-126 = -10-45 for 32-bit floating numbers or -2-52 * 2-1022 = -10-323 for 64-bit floating numbers.
Added April 20, 2009
IEEE 754 Floating Point Number representation:
0 is represented either by
1 00000000 00000000000000000000000
or by
0 00000000 00000000000000000000000
0.2 is represented by
0 01111100 10011001100110011001100
0.5 is represented by
0 01111110 10000000000000000000000
1.0 is represented by
0 01111111 10000000000000000000000
March 16, 2009
A NOTE ON COPY/REFERENCE SEMANTICS AND PASS BY VALUE/REFERENCE
Pass by value means passing the R-value.
Pass by reference means passing the L-value.
(See notes of Feb. 4 for discussion.)
Copy semantics in assignment means assigning the R-value of the source to the R-value of the target.
Reference semantics in assignment means assigning the L-value of the source to the L-value of the target.
Note 1: L-value is a reference to R-value.
Consider the following method Swap
static void Swap(Object x, Object y)
{
Object a;
a = x;
x = y;
y = a;
}
Here, x and y are passed by reference and reference semantics is used in the assignment
statements. Hence the method Swap does not swap the original
arguments because x and y passed to Swap are not references to x and y used in the
assignment statements.
Should x and y be passed by reference and copy semantics be used in the assignment
statements then method Swap would swap the original arguments, because x and y passed
to Swap would be the references to x and y used in the assignment statements. This
(automatic use of copy semantics while assigning objects), however, is not
achievable in Java.
Should x and y be passed by value, the reference semantics mandated by Java could not
be used in the assignment statements (out of lack of L-value), so method Swap would crash
(which is not the case here).
Should x and y be passed by value and copy semantics be used in the assignment
statements then method Swap would not swap the original arguments, because x and y passed
to Swap would be the references to x and y used in the assignment statements. This
(automatic use of copy semantics while assigning objects), however, is not
achievable in Java.
The above argument proves that Java passes object arguments by reference,
just like it uses reference semantics while assigning objects.
The following version of method Swap would swap the original arguments if the
dereferencing operator ^ were allowed:
static void Swap(Object x, Object y)
{
Object^ a;
a = x^;
x^ = y^;
y^ = a;
}
Since Java does not allow for the dereferencing operator ^, the closest scheme to the
above method that is expressible in Java is:
static void Swap(Object x, Object y)
{
Object a;
a = x.n;
x.n = y.n;
y.n = a;
a = x.m;
x.m = y.m;
y.m = a;
...
}
where n, m, ... are the instance variables of objects x and y. Here, the copy semantics is used in assignments,
so this Swap actually swaps the original arguments.
Note 2: The implicit parameter (referred to as this within the defining class) is subject to passing by reference as well.
Additionally, variable this is final so it cannot be the target of an assignment statement. This, in addition to a lack of
automatic use of copy semantics in assigning objects, is why I suggest the term protected pass by reference.
Exercise: Implement both methods in Java (no credit).
April 13, 2009
Section 13.1 Abstract Data Types
Linked
structures in languages like C and Pascal have been used to implement
recursively defined entities. For instance, a list can be recursively
defined as either an empty list (whatever it means) or a head followed
by a list (usually referred to as a tail).
Similarly, a stack can be recursively defined as an empty stack (whatever it means) or a top with a stack beneath it.
Java
is particularly well-suited for this kind of definitions, partially
because it does not allow manipulations of explicit pointers (or
L-values, if you will).
Here is a link to a simple Java class that defines list along the lines mentioned above:
http://csc.csudh.edu/suchenek/CSC321/List.java
where StudentInfo is defined here:
http://csc.csudh.edu/suchenek/CSC321/StudentInfo.java
A link to an abstract data type "singly-linked list" is here:
http://csc.csudh.edu/suchenek/CSC321/ADT_SLL.java
The
empty list is represented here by a dummy one-element list, called
header. It serves the purpose of providing an extra level of
indirection that is often needed in Java because of its pass-by-value (or
pass-by-protected reference, if you will) policy. For instance, method
makenull would be difficult to implement on empty list without the convention (use of
the header, that is).
Since the implicit argument is passed by
value (protected reference), empty recursive structure that admits
non-static method of type insert on it must not be a null value.
It must be an existing object, like, for instance, the header.
So, makenull makes sense under these circumstances.
Here is a link to a well-designed Java code that implements abstract data type stack:
http://csc.csudh.edu/suchenek/CSC321/StackL.java
Notice, how Java interpreter uses L-values and R-values, depending on the context, and you can't do anything about it.
How different it is in C. Here is a link to a C code that is as close to a well-designed Java code as possible:
http://csc.csudh.edu/suchenek/CSC321/StackL.c
Here, the L-values and R-values are explicitly handled by the programmer.
April 15, 2009
A link to example of inheritance and polymorphism in Java:
http://answers.yahoo.com/question/index?qid=20080907075234AAUTjmD
April 29, 2009
Reading, mandatory for the graduate students and optional for the undergreaduate students (skip the end of Section 4, page 28 to the end of section):
http://csc.csudh.edu/suchenek/CSC321/_NEGATIVE_INFO_DDB.pdf
The slides are here:
http://csc.csudh.edu/suchenek/CSC321/Logic_programming_vs_mathematical_logic.pdf
May 4, 2009
Resolution and unification
RESOLUTION
From p v q and r v ~q infer p v r
SPECIAL CASE (substitute ~s for p)
From ~s v q and r v ~q infer ~s v r
OR
From q :- s and r :- q infer r :- s
RESOLUTION FOR HORN CLAUSES
From A :- A1, A2, ... , An and B :- A, B1, ... , Bm
infer B :- A1, A2, ... , An, B1, ... , Bm
Example
mortal(X) :- man(X)
man(Socrates)
?- mortal(Socrates)
Example
bird(tweety)
flies(X) :- bird(X), ~abnormal(X)
?- flies(tweety)
abnormal(X) :- pinguin(X)
pinguin(tweety)
?- flies(tweety)
Example
Path(a, b)
Path(b, c)
Path(c, d)
Path(X, Y) :- Path(X, Z), Path(Z, Y)
?- Path(a, d)
UNIFICATION
Unify f(X, g(X, 3))
with f(h(Z), g(Y, Z)).
X = h(Z)
Unify f(h(Z), g(h(Z), 3))
with f(h(Z), g(Y, Z))
Y = h(Z),
Unify f(h(Z), g(h(Z), 3))
with f(h(Z), g(h(Z), Z))
Z = 3
Unify f(h(3), g(h(3), 3))
with f(h(3), g(h(3), 3))
A link to unification algorithm:
http://ale.cs.toronto.edu/docs/ref/ale_trale_ref/ale_trale_ref-node4.html
May 6, 2009
A link to GNU-Prolog manual:
PDF: http://www.gprolog.org/manual/gprolog.pdf
HTML: http://www.gprolog.org/manual/html_node/index.html
Program in file even.pl
even(0).
even(s(s(X))):-even(X).
even(2).
end_of_file.
Here is how to run it:
(The user input is highlighted red.)
[suchenek@dhcp-10-76-0-170 ~]$ gprolog
GNU Prolog 1.2.16
By Daniel Diaz
Copyright (C) 1999-2002 Daniel Diaz
| ?- [even].
compiling /home/suchenek/even.pl for byte code...
/home/suchenek/even.pl compiled, 4 lines read - 455 bytes written, 10 ms
yes
| ?- even(0).
yes
| ?- even(s(0)).
no
| ?- even(s(s(0))).
yes
| ?- even(X).
X = 0 ? ;
X = s(s(0)) ? ;
X = s(s(s(s(0)))) ? ;
X = s(s(s(s(s(s(0)))))) ?
(1 ms) yes
| ?- end_of_file.
[suchenek@dhcp-10-76-0-170 ~]$
==========================
Program in file cycle.pl
edge(1,3).
edge(2,3).
edge(2,4).
edge(4,1).
edge(4,0).
edge(4,3).
edge(6,5).
edge(6,8).
edge(8,9).
edge(9,6).
edge(5,7).
edge(7,6).
path(X,Y):-edge(X,Y).
path(X,Y):-path(X,Z),edge(Z,Y).
cycle(X):-path(X,X).
end_of_file.
Here is how to run it:
(The user input is highlighted red.)
[suchenek@dhcp-10-76-0-170 ~]$ gprolog
GNU Prolog 1.2.16
By Daniel Diaz
Copyright (C) 1999-2002 Daniel Diaz
| ?- [cycle].
compiling /home/suchenek/cycle.pl for byte code...
/home/suchenek/cycle.pl compiled, 20 lines read - 2330 bytes written, 60 ms
yes
| ?- cycle(X).
X = 6 ? ;
X = 6 ? ;
X = 8 ? ;
X = 9 ? ;
X = 5 ? ;
X = 7 ? ;
X = 6 ?
(1 ms) yes
| ?- end_of_file.
[suchenek@dhcp-10-76-0-170 ~]$
May 13, 2009
The correct meaning of a logic program; negation; nonmonotonic logic.
The statement in the textbook (page 414, lines 13, 12 from the bottom):
"h <-- p1,p2,...,pn.
This means that h is true only if p1,p2,...,pn are simultaneously true"
as well as the statement (page 417, line 2 from the bottom):
"Rules are interpreted as 'only if' assertions [...]"
are FALSE.
Consider logic program P:
bird(tweety).
bird(polly).
penguin(tweety).
flies(beetle).
flies(X):-bird(X),not penguin(X).
Here, beetle flies although bird(beetle) is not true, so not all literals in the body of the clause:
flies(X):-bird(X),not penguin(X).
are simultaneously true (so, according to the above statement from the textbook, flies(beetle) is false - a contradiction).
The correct definition of the meaning of a logic program requires the concept of minimal (Herbrand) model.
Ground terms:
{beetle, polly, tweety}
construction of a minimal Herbrand model:
Begin with facts:
{bird(polly), bird(tweety), flies(beetle), penguin(tweety)}
Query heads of bodied clauses for all ground terms.
:- flies(beetle).
yes
:- flies(polly).
yes
:- flies(tweety).
no
Add "yes" queries to the model:
{bird(polly), bird(tweety), flies(beetle), flies(polly), penguin(tweety)}
This is a minimal model of P (the "standard" minimal model of P).
In order to find other minimal models of P, let's consider a logically equivalent set of (non-Horn) clauses:
bird(tweety).
bird(polly).
penguin(tweety).
flies(beetle).
flies(X) v penguin(X):-bird(X).
Ground terms:
{beetle, polly, tweety}
construction of a minimal Herbrand model:
Begin with facts:
{bird(polly), bird(tweety), flies(beetle), penguin(tweety)}
Query heads of (non-Horn) bodied clauses for all ground terms.
:- flies(beetle) v penguin(beetle).
yes
:- flies(polly) v penguin(polly).
yes
:- flies(tweety) v penguin(tweety).
yes
Make sure one ground literal of each "yes" queries is in the model:
Results:
{bird(polly), bird(tweety), flies(beetle), flies(polly), penguin(tweety)}
{bird(polly), bird(tweety), flies(beetle), penguin(polly), penguin(tweety)}
These are the minimal models of P.
The query answering logic is non-monotonic.
Let's consider logic program Q:
bird(tweety).
bird(polly).
flies(beetle).
flies(X):-bird(X),not penguin(X).
Ground terms:
{beetle, polly, tweety}
construction of a minimal Herbrand model:
Begin with facts:
{bird(polly), bird(tweety), flies(beetle)}
Query heads of bodied clauses for all ground terms.
:- flies(beetle).
yes
:- flies(polly).
yes
:- flies(tweety).
yes
Add "yes" queries to the model:
{bird(polly), bird(tweety), flies(beetle), flies(polly), flies(tweety)}
This is a minimal model of Q (the "standard" one). Surprisingly, tweety flies in this model.
So, removing one assumption penguin(tweety) added an extra conclusion flies(tweety).
This strange attribute is called "nonmonotonic".
Other minimal models are:
{bird(polly), bird(tweety), flies(beetle), flies(polly), penguin(tweety)}
{bird(polly), bird(tweety), flies(beetle), flies(tweety), penguin(polly)}
{bird(polly), bird(tweety), flies(beetle), penguin(polly), penguin(tweety)}
More Prolog programs
[suchenek@csc208 ~]$ gprolog
GNU Prolog 1.2.16
By Daniel Diaz
Copyright (C) 1999-2002 Daniel Diaz
| ?- [user].
compiling user for byte code...
myappend([],X,X).
myappend([H|T],Y,[H|Z]):-myappend(T,Y,Z).
end_of_file.
user compiled, 3 lines read - 477 bytes written, 28380 ms
yes
| ?- myappend(X,Y,[a,b,c]).
X = []
Y = [a,b,c] ? ;
X = [a]
Y = [b,c] ? ;
X = [a,b]
Y = [c] ? ;
X = [a,b,c]
Y = [] ? ;
no
Comment. append(X, Y, Z) is a standard predicate in GNU Prolog.
| ?- append(X,Y,[a,b,c]).
X = []
Y = [a,b,c] ? ;
X = [a]
Y = [b,c] ? ;
X = [a,b]
Y = [c] ? ;
X = [a,b,c]
Y = [] ? ;
no
| ?-
Factorial
| ?- [user].
compiling user for byte code...
fact(N, 1):- (N is 0).
fact(N, Result) :- (N > 0), (M is N - 1), fact(M, P), (Result is N*P).
end_of_file.
user compiled, 3 lines read - 820 bytes written, 3020 ms
yes
| ?- fact(0,X).
X = 1 ? ;
no
| ?- fact(1,X).
X = 1 ? ;
no
| ?-
fact(4,X).
X = 24 ? ;
no
Factorial, with cut (!, highlighted yellow)
Note a lack of constrain (N > 0) in the second clause.
| ?- [user].
compiling user for byte code...
fact(N, 1):- (N is 0),!.
fact(N, Result) :- (M is N - 1), fact(M, P), (Result is N*P).
end_of_file.
user compiled, 3 lines read - 836 bytes written, 3453 ms
yes
| ?- fact(0,X).
X = 1
yes
| ?- fact(4,X).
X = 24
yes
Comment. The meaning of the query
fact(N, Result) :- (M is N - 1), fact(M, P), (Result is N*P)
is:
fact(N, Result) :- there exist M and P such that: (M is N - 1), fact(M, P), (Result is N*P)
Bubble sort
| ?- [user].
compiling user for byte code...
mysort(L, S) :- append(U, [A, B|V], L), (B < A), !,
append(U, [B, A|V], M), mysort(M, S).
mysort(L, L).
end_of_file.
user compiled, 5 lines read - 946 bytes written, 2914 ms
(1 ms) yes
| ?- mysort([2,1,3,5],X).
X = [1,2,3,5]
yes
| ?-
Go to the top.
|
|