|
|
|
Last revised September 9, 2018
The
contents of this website, the links contained therein directly and
indirectly, and the contents of the said links, are copyrighted.
They are provided exclusively for
non-profit educational use by the students currently enrolled in this
course and for the duration of this semester. No other use or any use
by others is allowed
without authorization of the professor in this course and copyright
holder or holders.
Homework
The Homework page is subject to change as I will cover the course material. You
are
welcome to do your homework in advance, but by doing so you accept the
risk
that the homework you have done might have been changed or deleted.
Some
test and final questions may be similar to some homework problems,
so although homework yields no credit (unless noted otherwise), doing
all homework is likely to help you get a better grade in this course.
Click
here for the most recent homework.
Chapter 1
No credit
assignment:
0. Pove by mathematical induction on n that
for every integer n > 0 and every integer k > 0 with k <= n,
#{k,
k+1, ..., n} = n - k + 1,
where #X is the cardinality (the number of
elements, that is) of X.
1. Prove that if f(n) is an increasing function then the
following implication holds:
f(x) < f(y) => x < y
2. Prove that floor(x) is less than or equal to ceiling(x).
3. If you understood the proof in
http://csc.csudh.edu/suchenek/CSC401/Mathematica/Proof_floorLog2eqCeilLog2Plus1.nb
(presented in class) then:
Prove (without looking into the above file) that for any integer number
b > 1 and any integer number n > 0,
floor(logb n) + 1 = ceiling(logb (n + 1)) .
If you have difficulties with it, try first to prove the above for b =
3, and then for b = 10.
4. Pove that for every integer n:
floor(n/2)
+ ceiling(n/2) = n
5. Page 61 and on.
Problems 1.1, 1.2, 1.5, 1.6, 1.7, 1.8, 1.12, 1.14, 1.22., 1.23, 1.27,
1.28, 1.30, 1.31 a, 1.39, 1.40, 1.43, 1.44.
6.
Homework on probability: http://csc.csudh.edu/suchenek/CSC401/Montel_Puzzle.html
7. The printout
of the result of execution of the Binary
Search program (Java)
(both were posted in Lecture Notes here, with some helpful
explanation of the formulas used in the said program)
has some lines that might suggest that the theoretic lower and the
upper bound on the average number of comparisons while successfully
searching an n-element ordered array were incorrect. For instance, this
one:
Avg = 7.527859237536657
Approximate low value of avg = 7.417852514885897
Approximate high value of avg = 7.517852514885897
Does NOT fit in!
a.
Explain the mentioned above discrepancy, providing detailed
calculations that support your explanation.
b.
Modify the said program so that the correct (or more accurate) values
that it prints do not suggest that there is a discrepancy between the
computed average and the theoretic bounds. Run the said program and
verify its correctness by inspection of its output.
Hint:
Study carefully the derivation of the said bounds done in file http://csc.csudh.edu/suchenek/Mathematica/AverageTimeBinSearch.pdf
Chapter 4,
Analysis of InsertionSort
No credit
assignment:
1.
Find two different worst-case arrays E with 10 elements for
InsertionSort. Prove that your answer is correct while computing the
exact numbers of comparisons of elements of E that InsertionSort will
perform while sorting E.
2. Compute
the average number of comparisons for inserting:
1st
element
2nd element
3rd element
4th element
first 4 elements
Use formulas
from Mathematica notebook InsertionSortAvgTime.nb
3.
Consider modified version SneakySort of InsertionSort that compares the
(i+1)st element x to E[0] first, then, if greater than, to E[1], and so
on, and after finding index j for insertion of x shifts the current
elements E[j], E[j+1],..., E[i] one position up (if j <= i).
a. How many
comparisons of elements of E will SeakySort perform while sorting an
anti-sorted array E with n elements?
b. How many
inversions will SeakySort remove while sorting an anti-sorted array E
with n elements?
c. Is
SneakySort an element of class C defined in class (and in Mathematica
notebook InsertionSortOptimality.nb)?
d.
Derive the average number of comparisons S(n) of elements of E that
SneakySort will perform while sorting an array with n
elements.
Example code
for SneakySort:
public
static void SneakySort(int[] E)
{
int
n = E.length;
if
(n < 2) return;
for
(int i = 1; i < n; i++)
{
int
j = 0;
while
((j < i) && (E[j] < E[i])) j++;
if
(j < i)
{
int
x = E[i];
for
(int k = i; k > j; k--) E[k] = E[k - 1];
E[j]
= x;
}
}
}
See:
http://csc.csudh.edu/suchenek/CSC401/Programs/QuickSort/Inversions/src/inversions/
SneakySort.java
http://csc.csudh.edu/suchenek/CSC401/Programs/QuickSort/Inversions/src/inversions/cnt.java
http://csc.csudh.edu/suchenek/CSC401/Programs/QuickSort/Inversions/src/inversions/cnt2.java
Chapter
4,
Analysis of QuickSort
No credit
assignment:
1.Find
3 different worst-case arrays E with 7 elements for Quicksort (each of
them must be a permutation of numbers 1, 2, 3, 4, 5, 6, 7) and execute
QuickSort (on paper) on one of them. How many inversions does each E
have? How many
comparisons did QuickSort made? How does it compare to theoretic
average?
2.
Find a best-case array E with 15 elements for Quicksort and execute
QuickSort (on paper) on E. How many inversions does E have? How many
comparisons did QuickSort made? How does it compare to theoretic
average?
Chapter
4, Analysis of MergeSort
No credit
assignment:
1. Exercise
4.26 p. 212
2. Execute
Mergesort (on paper) on an anti-sorted sequence E of 15
elements. How many inversions does E have? How many
comparisons did MergeSort made? How does it compare to theoretic
worst-case?
3. Find a 15-element array (a permutation of numbers 1, 2, 3,..., 14, 15) that is a worst-case array for MergeSort.
4. Find a 15-element array (a permutation of numbers 1, 2, 3,..., 14, 15) that is a best-case array for MergeSort.
5. What is
the necessary and sufficient condition for the subarrays that are to be merged which
will force Merge to perform the maximum number (n - 1, that is) of
comparisons of keys? Answer.
6. Draw the
recursion tree T for MergeSort for n = 15. How many comparisons of keys
were made in the worst case at each non-empty level of T? How many comparisons of keys were made in the best case at each non-empty level of T?
7. Show that the depth of the recursion tree for MergeSort for any n >= 1 is equal to ceiling(lg n).
Chapter
4, Lower Bounds for sorting
No credit
assignment:
1. Exercises
4.31 and 4.32 a. p. 213
2. Draw
decision trees with n = 3 for these sorting algorithms:
- InsertionSort
- MergeSort
What are the
hights of these decision trees?
3.
Using Stirling's formula and Lemma 4.8 p. 179, prove that the lower
bound on the number of comparisons needed to sort an n-element array
(by comparisons of keys) is
(n
+ 1/2) log2 n - 1.45 n + 0.91.
4. What is
the shortest external path length in a 2-tree with m leaves?
5. What is
the shortest external path length in a 2-tree with n nodes?
Chapter
4,
Analysis of HeapSort
No credit
assignment:
1. Exercises
4.34, 4.35, 4.36, and 4.42 a. p. 212 - 213.
2. Using
Mathematica, graph function f(x) = x
log2 x
for x ranging from 0.001 to
20.0.
3. Using
Mathematica, prove that function f(x)
= x log2 x
is a convex function by
showing that its second derivative is > 0.
4. Derive a
formula on the number of decimal digits that are needed to write an
integer number n > 0?
5. What is
the value of the formula that occurs in the subtitle of Figure 7 in the
lecture note "Heaps and Balanced Trees" (http://csc.csudh.edu/suchenek/CSC401/Balanced_tree.pdf)? Calculate that value in two
different ways using Mathematica.
6. Using
Mathematica, show that the formula for Sn-1
given by equation (2) in the
lecture note "Heaps and Balanced Trees" (http://csc.csudh.edu/suchenek/CSC401/Balanced_tree.pdf) is correct by graphing the
left-hand side and the right-hand side together on the same graph.
7. Using
Mathematica, show that function CMakeHeap(n) in the inequality (8) in the
lecture note "Heaps and Balanced Trees" (http://csc.csudh.edu/suchenek/CSC401/Balanced_tree.pdf) is in 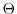 (n)
(big theta of n). Use both: the Limit[...] operation of Mathematica and
graphing of the left-hand side, the right-hand sand of the inequality
(8) on the same graph together with function f(n) = c*n for
appropriately chosen constant c.
Chapter
5,
Selection and Adversary Arguments
No credit
assignment:
1. Show that
for even n:
n
+ ceiling(n/2) - 2 = (3/2)n - 2
and that for
odd n:
n
+ ceiling(n/2) - 2 = (3/2)n - 1.5.
2. Show that
for any integer n,
ceiling(n/2) + floor(n/2) = n
Use the above equality to calculate:
a) n -
2*floor(n/2)
b)
2*ceiling(n/2) - n
3.
Prove that if the tournament method is used to find Max (without
finding SecondMax) among n distinct key then exactly n - 1 comarisons
are made. (We know from the lower bound proved in class before that at
least n - 1 comparisons have to be made, but it is less than saying
that exactly n - 1 comparisons are made.)
4. Exercises
5.1., 5.3, and 5.5 a. page 242.
5. Now, prove Theorem 5.1 p.
226 and Theorem 5.2 p. 230.
Chapter 7
No credit
assignment:
Page 375 and on,
Exercises 7.1, 7.4 (a, b), 7.5 (a, b), 7.12.
Chapter
8
No credit
assignment:
1. Pages 416 ...
Exercises 8.1, 8.6, 8.8, 8.12, 8.13, 8.14, 8.15, 8.24.
2.
Give one example of a set of connected
graphs of unlimited size (in terms of the number of vertices) for which
the (faster version of) Prim's MST algorithm is faster in the worst
case (by means of big Theta notation) than the (faster version of)
Kruskal's MST algorithm, and one example of a set for which Kruskal's
is faster than Prim's. Justify your answer by appropriate use of big
Theta characterizations of the worst-case running times of these
algorithms.
3. Let G be a
connected weighted graph and T be its spanning tree. Let
e be an edge in G but not in T that has smaller weight w than any edge
in T. Prove that T is not a MST of G.
4. Prove
Lemma 8.8 page 413.
5. Prove
Theorem 8.9 page 413.
Chapter 10
No credit
assignment:
1. Page 477
Exercises 10.2 10.8, 10.9, 10.10.
2. Derive the exact formula for the average
number of comparisons of
keys while sucessfully searching for a key in an optimal binary search
tree with n nodes under the assumption that probability of searching
for each key is the same (equal to 1/n). Hint. Find the formula for the minimal internal path length ipl(n) of a tree with n nodes in the lecture
notes and note that the
average number of comparisons while sucessfully searching for a
key in a shortest ("completely
balanced" according to text's
terminology) binary search tree T with n nodes is: 1 + ipl(n) / n.
3. Derive this recurrence
relation:
A[i][j] =
A[i][k - 1] + A[k + 1][j] + p(i, j)
where 1 <= i < j
<= n, k is the index of the root of a subtree T of an optimal
BST with nodes K1, ..., Kn,
and the nodes of U are Ki, ..., Kj.
Chapter 13
No credit
assignment:
1. Prove that the Coloring
Graph Problem is polynomally reducible to the CNF Satisfiability
Problem.
2. List all
the P problems mentioned in
Chapter 13. (There were several!)
3. List all
the NP problems mentioned in Chapter 13 that are not known to be in P.
4. List all the NP-complete
problems mentioned in Chapter 13.
5. Page 600
...
13.2, 13.4.c, 13.12, 13.55.
|
|
