Natki z wykladu
Preliminaria matematyczne
Pojecie zbioru
rownosc, rownolicznosc, zbiory skonczone, przeliczalne
http://matematyka.pisz.pl/strona/1058.html
http://matematyka.pisz.pl/strona/1059.html
http://pl.wikibooks.org/wiki/Matematyka_dla_liceum/Liczby_i_ich_zbiory
Operacje na zbiorach:

Wyjasnienie paradoksu golibrody (Barber's Paradox) jako eleganckiego dowodu ze kazdy zpior ma wiecej podzbiorow niz elementow:
http://csc.csudh.edu/suchenek/Papers/Cantor_barber_Russell.doc
Wyrazenia logiczne
http://matematyka.pisz.pl/strona/1071.html
Kwantyfikatory
Zasada indukcji matematycznej
definiowanie przez indukcje
http://pl.wikipedia.org/wiki/Indukcja_matematyczna
Rekurencja
http://pl.wikipedia.org/wiki/Rekurencja
Listy
Indukcyjna definicja listy:
http://csc.csudh.edu/suchenek/wwsi/Def_list.pdf
Drzewa
drzewo binarne, pelne, completne, wlasnosci drzew
http://pl.wikipedia.org/wiki/Drzewo_(matematyka)


Definicje i wlasnosci drzew:
http://csc.csudh.edu/suchenek/wwsi/Def_tree.txt
Macierzowa reprezentacja kompletnego drzewa binarnego jako zbioru ciagow binarnych:
http://csc.csudh.edu/suchenek/wwsi/TreeSequentialRepresentation.pdf
Definicja drzewa poszukiwan binarnych:
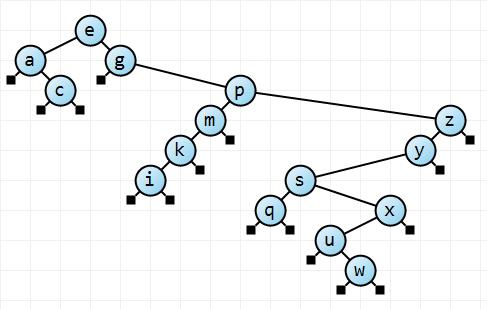
http://csc.csudh.edu/suchenek/wwsi/Def_BS_tree
http://edu.i-lo.tarnow.pl/inf/utils/002_roz/mp001.php

Grafy
http://pl.wikipedia.org/wiki/Graf_(matematyka)
Mathematica
Rekurencja
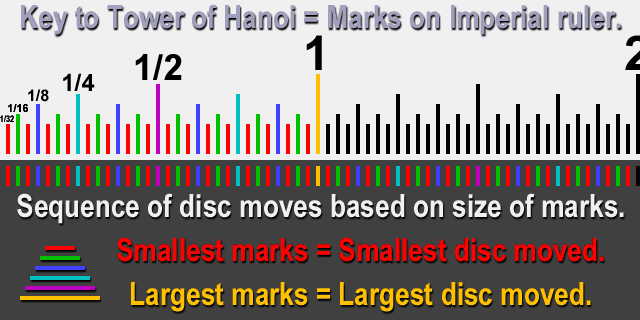
Wieże Hanoi
http://wazniak.mimuw.edu.pl/images/9/91/kontener.html?nazwa_animacji=/images/c/c3/Wieza_hanoi
http://wazniak.mimuw.edu.pl/index.php?title=Matematyka_dyskretna_1/Wyk%C5%82ad_2:_Rekurencja
Ciekawe rozwiazanie zagadki (rysunek pochodzi z http://pballew.blogspot.com/2011/01/neat-solution-to-towers-of-hanoi.html ):
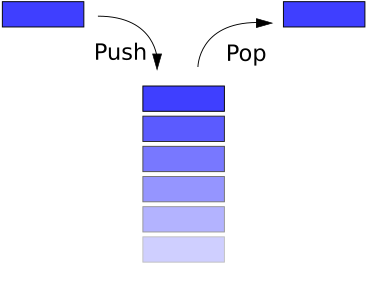
Stack (stos)
Operacje: construct, push, pop, i isEmpty?
Queue (kolejka)
Operacje: construct, enqueue, dequeue, isEmpty

Liniowa reprezentacja kolejki cyklicznej:

Inkrementacja front i rear odbywa sie modulo capacity (pojemnosc kolejki). Java syntax:
front = (front + 1) % capacity
rear = (rear + 1) % capacity
My uzywac bedziemy "out" (wyjscie) zamiast "front" i "in" (wejscie) zamiast "rear".
ADT TREE
Wlozenie do drzewa poszukiwan binarnych:


Sekwencja wlozen do pustego drzewa poszukiwan binarnych:

Usuwanie z drzewa poszukiwan binarnych:

Zlozonosc obliczeniowa operacji na drzewach:
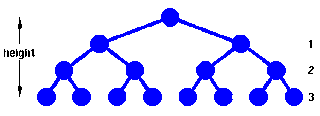
Drzewo niezbalansowane:

Drzewo zbalansowane:
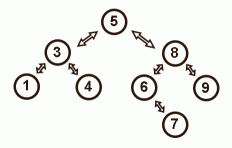
Przypadkowe drzewo poszukiwan binarnych:

Dlugosc sciezki zewnetrznej i sciezki wewnetrznej:
http://csc.csudh.edu/suchenek/wwsi/External_internal_path.pdf
Liczba drzew binarnych o n wiezcholkach = liczba Catalana:
http://en.wikipedia.org/wiki/Catalan_number
Liczba permutacji n elementow = n!
Przyklady obliczen wysokosci drzew binarnych oraz kosztow operacji na typowych drzewach:
http://csc.csudh.edu/suchenek/wwsi/Balanced_tree.pdf
Liczba niskich drzew wyszukiwania binarnego:
http://csc.csudh.edu/suchenek/wwsi/Explicit_number_of_best_BST.pdf
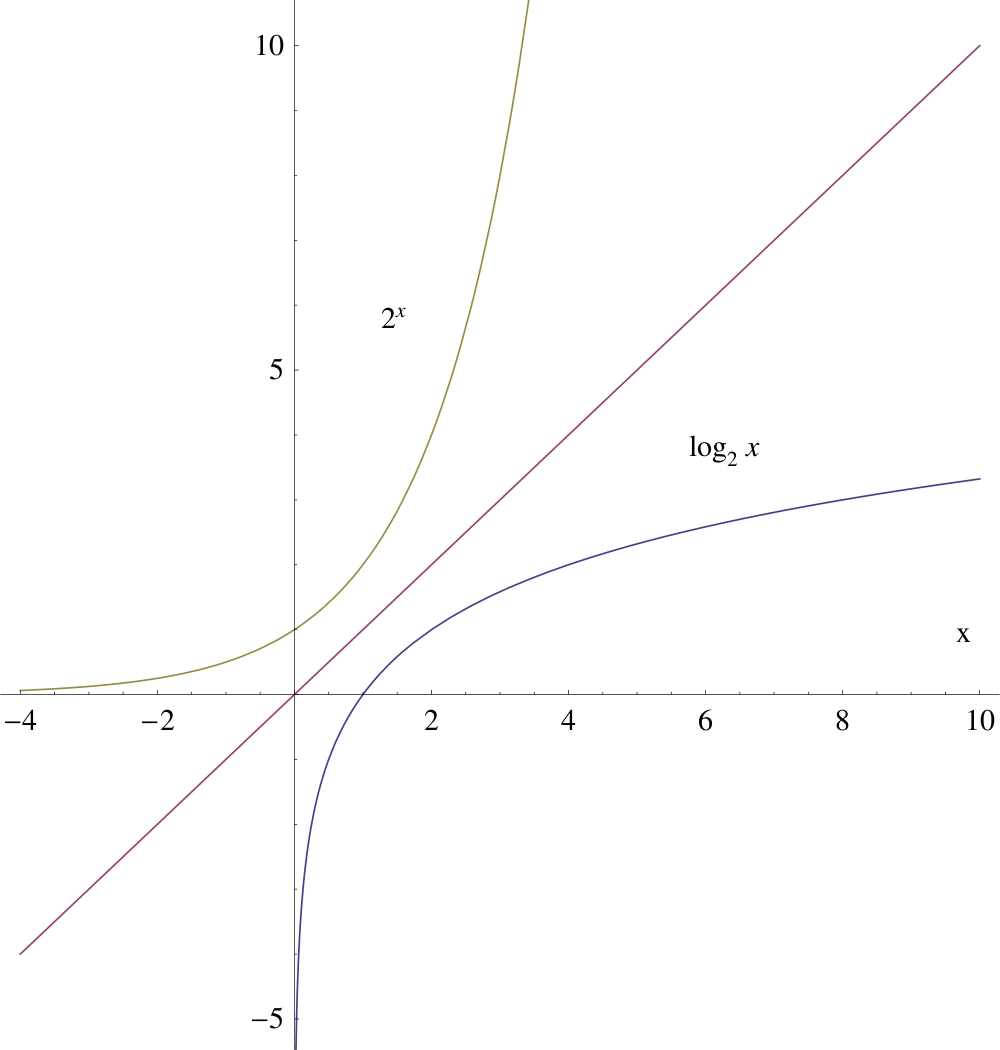
Wykresy funkcji wykladniczej i logarytmu przy podstawie 2:
ADT GRAPH (graf)
Przyklad pozornie prostego problemu grafowego wymagajacego dlugotrwalych obliczen:
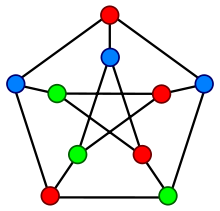
Kolorowanie wierzcholkow grafu.
Zastosowania grafow w rozproszonych bazach wiedzy:
http://csc.csudh.edu/suchenek/wwsi/Suma_Iloczyn_zagadka.pdf
Szacowanie zlozonosci problemow
public static int f(int n)
{
if (n <= 1) return 1;
if (n%2 == 0) return (f(n/2) + 1);
else return (f(3*n + 1) + 1);
}
It is not known whether the above program always halts or falls into an endless loop for some integer n.
Definicje i wlasnosci notacji "Duze O"
http://csc.csudh.edu/suchenek/wwsi/BigOh1.pdf
http://csc.csudh.edu/suchenek/wwsi/BigOhAllSmall3-500.pdf
http://csc.csudh.edu/suchenek/wwsi/BigOhAllShort2-10.pdf
http://csc.csudh.edu/suchenek/wwsi/WorstAvgRunTime.htm
http://csc.csudh.edu/suchenek/wwsi/AverageTimeBinSearch.htm
http://csc.csudh.edu/suchenek/wwsi/BSearchDecisionTree.htm
Funkcja Ackermanna - rosnie szybciej niz cokolwiek co mozesz precyzyjnie zapisac w notacji matematycznej.
This is a well tested program that computes one value of 3-argument Ackerman's function.
1st and 2nd argument are the numbers on which a two-argument operation is to be carried out.
3rd argument is an index of the operation.
E.g., A(k, m, 0) = k + m
A(k, m, 1) = k * m
A(k, m, 2) = k ^ m
etc.
*/
public class Ackerman3arg
{
static long count = 0;
public static void main (String [] args)
{
// int n = Integer.parseInt(args[0]);
// int m = Integer.parseInt(args[1]);
// int k = Integer.parseInt(args[2]);
long n = 2;
long m = 2; //second arg of "the" Ackermann's function
long k = 3; //first arg of "the" Ackermann's function
long a = A(2,m + 2, k - 1) - 3;
System.out.print("A(" + n +
", " + m + ", " + k + ") = " + a);
System.out.println(" count = " + count);
}
public static long A(long k, long m, long n)
{
// count++;
if (n == 0) return m + k;
else
{
if (m == 0)
{
if (n == 1) return 0;
else
{
if (n == 2) return 1;
else return k;
}
}
else return A(k, A(k, m-1, n), n-1);
}
}
}
/*
A(k, m, 0) = m + k;
A(k, 0, 1) = 0
A(k, 0, 2) = 1
A(k, 0, n+3) = k
A(k, m+1, n+1) = A(k, A(k, m, n+1), n)
*/
/*
Note: "the" Ackermann function (with a simpler recurrence relation) refers to:
A(2, n+2, m-1) - 3
*/
|