|
|
|
Last revised January 29, 2015
The
contents of this website, the links contained therein directly and
indirectly, and the contents of the said links, are copyrighted.
They are provided exclusively for
non-profit educational use by the students currently enrolled in this
course and for the duration of this semester. No other use or any use
by others is allowed
without authorization of the professor in this course and copyright
holder or holders. No
videotaping or recording without professor's prior permission is
allowed in class.
Lecture Notes
These Lecture Notes
are subject to change as I will cover the course material. You are
welcome to read them in advance, but by doing so you accept the risk
that the notes you have read might have been changed or deleted.
Click here for the current
posting.
Use of
Mathematica by the students is strongly recommended (but not required).
Here
are
my
slides
on
how
to use Mathematica help:
http://csc.csudh.edu/suchenek/CSC311/Slides/Mathematica_instructions.pdf
January 20,
2015
Here is a link to slides, Appendix B:
http://csc.csudh.edu/suchenek/CSC311/AppB_excerpts_comments.pdf
and
http://csc.csudh.edu/suchenek/CSC311/Slides/AppA.pdf
Slides:
http://csc.csudh.edu/suchenek/CSC311/Def_big_Oh_big_Theta_slides.pdf
It's a copyrighted
material, so the students in this class can read them but not to
copy or distribute them.
The
main objective of this chapter (big "oh" notation and related issues)
is to introduce a mathematical tool that would allow for meaningful
evaluation of performance of future
programs.
Telling
the efficient (whatever it means) programs from inefficient ones is
about as important as telling high-yield investments from low-yield
investments.
An invalid claim that a solution to a sluggish
program is to run it on a faster computer is about as "rational" as an
advise that in order to increase yield on low-yield investment one
needs to invest more money in that sluggish enterprise.
Because
we are talking future and predictions, we must use an abstract
(implementation- and technology-independent) "yardstick" with which to
measure program's performance as a function of the size of its input.
Examples
of
abstract "yardstick":
- an unspecified "running time",
- number of times all the innermost
loops have been
traversed,
- number of memory accesses,
- number of (bytes of) external
transfers.
One can use similar method to evaluate the space performance (memory demand)
of a program.
In this class we will focus mostly on time
performance, though.
The second issue related to measuring is what "yardstick" to use in
order to describe the size of the input to the program.
For
instance, if a program in question tests primality of an integer number
of arbitrary size then it's running
time
is
a
function
of the "size" of
its input. Typically, the "larger" the size of the integer to be
tested
the more time the program may need in order to determine if that number
is prime or not.
Question:
What is
the size of number 1,951? 1,234,567,891? Why?
Here
is a link to slides with derivation of the formula on the number of
bits needed to represent a positive integer M:
http://csc.csudh.edu/suchenek/CSC311/Size_of_integer_M.pdf
It's equal to:
floor(lg2
M) + 1
A
primality test program reads an input integer number n > 1 and attempts no more
than sqrt(n) - 1 division before deciding if n is prime or not.

The maximum number of divisions is
floor(sqrt(n) - 1) = floor(sqrt(n)) - 1.
where floor is defined
here:
http://csc.csudh.edu/suchenek/CSC311/FloorCeilingLog2.jpg
So,
if the size of n is
m =
floor(flog_2 n) + 1,
or is the least m that satisfies this inequality:
n
<= 2^m - 1 (2 to power m
minus 1 = the largest number with m bits),
then the
running time T(m) of this primality test program is:
T(m) = floor(sqrt(n)) - 1 <= floor(sqrt(2^m - 1)) - 1
= ceiling(2^(0.5m)) - 2 =
[approx.] 2^(0.5m) - 1
(= 2 to power m half).
It turns out that actually for every m > 0 there is n > 0 of size
m such that
T(m) = floor(sqrt(2^m - 1)) - 1,
not just <=
floor(sqrt(2^m - 1)) - 1. The
program posted on page Programs experimentally verifies that equality.
So,
the running time of this program is an exponential function. In
other
words, except for relatively small inputs (of the size, say, no more
than 150 decimal digits), this program is impractical as it will
require humongous amount of time (much more than one year on a 1
petaflops/sec supercomputer) to complete the task.
Hints: 1 year = (approx.) 3*10^7 sec.
1
petaflops = 10^15 flops.
In addition of some programs being impractically slow, it may be very
difficult to tell a fast one from a sluggish one, even if they are
short and "simple".
Mathematica
calculations
of
the
running
time of the above program
http://csc.csudh.edu/suchenek/CSC311/Mathematica/PrimTestRunningTime.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/PrimTestRunningTime.pdf)
Here is a "simple" recursive program whose
performance appears
very hard to evaluate:
public static int f(int n)
{
if (n <= 1)
return
1;
if (n%2 == 0)
return
(f(n/2));
else return
(f(3*n + 1));
}
For instance, the execution trace for n = 15
is:
n:
15,
46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1.
It
is
not known whether the above program always halts or falls into an
endless loop for some integer n. Here is a link to a paper that reports
on fairly recent status on the research on that problem:
http://www.ams.org/bookstore/pspdf/mbk-78-prev.pdf
Example
from the textbook:
Selection Sort

Here is a link to one of the slides I
discussed in class - computation
of the number of times that the body of the innermost loop in the SelectionSort method is traversed:
http://csc.csudh.edu/suchenek/CSC311/RunTimeSelectionSort.pdf
Mathematica
notebook doing the
same:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/InsertionSortTime.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/InsertionSortTime.pdf)
February 5,
2015
Function and its inverse:
 
Logarithms at various bases:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/LogsVar.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/LogsVar.pdf)
Worst-case and average-case running times:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/WorstAvgRunTime.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/WorstAvgRunTime.pdf)
Definition of big
Oh, big Theta, and little oh:
http://csc.csudh.edu/suchenek/CSC311/Def_big_Oh_big_Theta.pdf
Slides:
http://csc.csudh.edu/suchenek/CSC311/Def_big_Oh_big_Theta_slides.pdf
Relationship
between
the
running
time
and
the maximum size of input (recommended
reading):
It's a copyrighted
material, so the students in this class can read it but not to
copy or distribute it
http://csc.csudh.edu/suchenek/CSC311/Big_Oh_new_with_reciprocal_measures.pdf
Slides:
http://csc.csudh.edu/suchenek/CSC311/Big_Oh_new_with_reciprocal_
measures_slides.pdf
and excerpts (the minimum on
this topic that all students are responsible for in addition to
the contents of the Appendix B in the textbook):
http://csc.csudh.edu/suchenek/CSC311/Big_Oh_ez.pdf
Examples for big "Oh"
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh2.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh2.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh2_1.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh2_1.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh2_2.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh2_2.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh3.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh3.pdf)
Exercises:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh_exercise.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOh_exercise.pdf)
Fact:
O(f(n) +
g(n)) = O (max(f(n), g(n)).
Illustration:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/MaxBigOh.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/MaxBigOh.pdf)
Growth rates of functions:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll1-3.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll1-3.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll1-5.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll1-5.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll1-7.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll1-7.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-10.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-10.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-20.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-20.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-30.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-30.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-40.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-40.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-200.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAll2-200.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAllShoer2-10.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAllShoer2-10.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAllSmall3-500.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhAllSmall3-500.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhExp.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhExp.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLog1.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLog1.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLog2.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLog2.pdf)
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLog3.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLog3.pdf)
These links are optional:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLogDif.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLogDifExp.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLogDifExp2.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLogExp.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhFloorLogExpDif.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BigOhLogVsPoly.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/FloorCeilLog2Dif.nb
Here is
a link to a
program that evaluates its own running time:
http://csc.csudh.edu/suchenek/CSC311/quadratic/Main.java
Here is a link to Mathematica notebook with
analytic computation of the
same:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/QadraticTime.nb
(PDF: http://csc.csudh.edu/suchenek/CSC311/Mathematica/QadraticTime.pdf)
February 12,
2015
Hanoi
Towers Animation:
http://wazniak.mimuw.edu.pl/images/9/91/
kontener.html?nazwa_animacji=/images/c/c3/Wieza_hanoi
Interesting solution using imperial ruler:

The running time T(n) of Hanoi Towers
solution for n disks is double-exponential!
T(n) = 2^n
- 1
See the comment after program in file http://csc.csudh.edu/suchenek/CSC311/Hanoi/Main.java
for proof.
But
size(n) = Floor(lg n) + 1 = approx. lg n,
or
n
= approx. 2^size(n).
So,
T(size(n))
= 2^n - 1 = approx 2^(2^size(n))
-
1.
It may also be proved that the mentioned above solution is optimal,
that is, it cannot be found in less than 2^n - 1 moves.
In other words, the size of the shortest ouput for any solution of the
Hanoi towers problem is 2^n - 1.
So, the mentioned above solution is linear in the size
of output.
February 17, 2015
Priority Queue
ADT PRIORITY QUEUE:
http://csc.csudh.edu/suchenek/CSC311/PriorityQueueIntro.pdf
PQ Sort:
http://csc.csudh.edu/suchenek/CSC311/Running_time_PQSort.pdf
Sorted array implementation
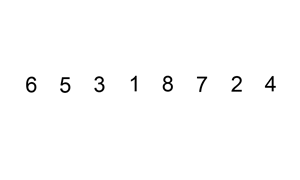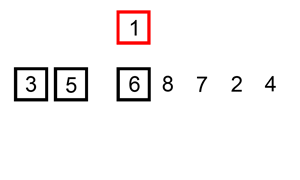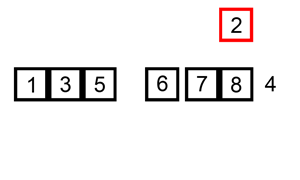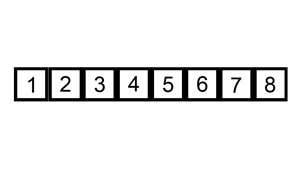
Linked implementation:
http://csc.csudh.edu/suchenek/CSC311/PriorityQueueImplementationLink.pdf
http://csc.csudh.edu/suchenek/CSC311/Def_list.pdf
Resizing
and its cost for array implementation:
http://csc.csudh.edu/suchenek/CSC311/resizing.pdf
Mathematica made it easier:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Cost_resizing.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Cost_resizing_playbox.nb
PDF output of the above:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Cost_resizing.pdf
March 10, 2015
Chapter
6
Link
to
slides: http://csc.csudh.edu/suchenek/CSC311/Slides/StacksQueues.pdf
It's a
copyrighted
material, so the students in this class can read them but not to copy or distribute
them.
ADT
STACK

Image from
http://files.myopera.com/malifarsi2/blog/2000px-Data_stack_svg.png
More
examples of stacks:
For a rainy day Java's stack of activation records More for a rainy day For the learned Official Human In creation ... Double stack Workout Rock stack Compuer
stack Hardware stack Software stack Really good stack
ADT
QUEUE

http://aplcenmp.apl.jhu.edu/Classes/Notes/Felikson/courses/605202/lectures/L4/
page15.JPG

http://aplcenmp.apl.jhu.edu/Classes/Notes/Felikson/courses/605202/lectures/L4/
page15b.JPG

http://aplcenmp.apl.jhu.edu/Classes/Notes/Felikson/courses/605202/lectures/L4/
page17.JPG

http://www.math.bas.bg/~nkirov/2012/NETB201/slides/ch04/ch04.html
The figure below is a modification of http://cs.nyu.edu/~gottlieb/courses/2004-05-fall/alg/class-notes.html

An error
in Program 6.22
Circular Queue Representation page 185 of the
textbook:
http://csc.csudh.edu/suchenek/CSC311/Error_in_queue.pdf
One example of use of ADT QUEUE:
http://csc.csudh.edu/suchenek/CSC311/Traversal2.jpg
March 24, 2015
ADT LIST
A definition of ADT LIST:
http://csc.csudh.edu/suchenek/CSC311/ADT_LIST.TXT
Insert
to an
delete from a LIST implemented as an array:

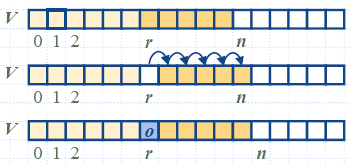
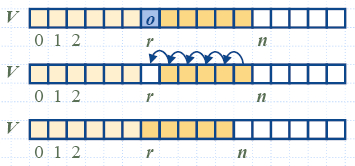
(Above figures are from:
http://www.math.bas.bg/~nkirov/2007/NETB201/slides/ch05/ch05.html)
A definition of
(singly-linked) list:
http://csc.csudh.edu/suchenek/CSC311/Def_LIST_POSITION
POSITION
and
Insert:
http://csc.csudh.edu/suchenek/CSC311/SLL_POS_and_Insert.pdf
http://csc.csudh.edu/suchenek/CSC311/SLL_POS_and_Delete.pdf
A definition of doubly-linked list:
http://csc.csudh.edu/suchenek/CSC311/Axiomatic_def_DLL.txt

https://staff.fnwi.uva.nl/a.j.p.heck/Courses/JAVAcourse/ch4/sss1_2_3.html

http://rpmedia.ask.com/ts?u=/wikipedia/commons/0/07/Doubly_linked_list_insert_after.png
The following are
my modification of the linked above material. It's
all a copyrighted
material, so the students in this class can read them but not to copy or distribute
them.
This link has been
temporarily disabled:
http://csc.csudh.edu/suchenek/CSC311/Slides/DLL_insert.pdf
April 16, 2015
Trees
Link
to slides:
http://csc.csudh.edu/suchenek/CSC311/Slides/Trees.pdf
It's a copyrighted
material, so the students in this class can read them but not to copy or distribute
them.
Three definitions of tree
and its properties:
http://csc.csudh.edu/suchenek/CSC311/Def_tree.txt
Sequential representation of contiguous binare tree viewed as a set of
binary sequences:
http://csc.csudh.edu/suchenek/CSC311/TreeSequentialRepresentation.pdf
Here is a link to a rigorous
computation
of
the
running
times of insert and remove on heaps; Sections 1.1 through 1.6. are
mandatory readings; details of calculations/derivations in Sections
1.7 through 1.9 are optional, but the students are responsible for
all "big
Theta" facts:
It's a copyrighted
material, so the students in this class can read them but not to copy or distribute
them.
http://csc.csudh.edu/suchenek/CSC311/Balanced_tree.pdf
Here are the slides for the above; Sections 1.1 through 1.6.
are mandatory readings; details of calculations/derivations in Sections
1.7 through 1.9 are optional, but the students are responsible for
all "big
Theta" facts:
It's a copyrighted
material, so the students in this class can read them but not to copy or distribute
them.
http://csc.csudh.edu/suchenek/CSC311/Balanced_tree_slides.pdf
Animation that explains how heap is used in sorting:
Note: The bottom line is
that you are supposed to study and
understend the Java code posted on class website. This
animation visualizes in some detail the idea of heapsort. Actual
details in the Java code posted on class website may be slightly
different.

http://upload.wikimedia.org/wikipedia/commons/4/4d/Heapsort-example.gif
Optional:
Another website with animation
(continuous
or
step-by-step)
of Heapsort
with fast heap-construction phase:
http://www.ee.ryerson.ca/~courses/coe428/sorting/heapsort.html
Animation that shows how Heapsort sorts:
http://upload.wikimedia.org/wikipedia/commons/1/1b/Sorting_heapsort_anim.gif
Optional:
Mathematica calculations of the sum of floors of
logarithms base 2 of consecutive integers (used to compute running times of
insert and remove on heaps):
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Heap_performance.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Heap_performance.pdf
Tree
traversal:
http://www.cosc.canterbury.ac.nz/mukundan/dsal/BTree.html
Programs from textbook:
http://csc.csudh.edu/suchenek/CSC311/Traversal1.jpg
http://csc.csudh.edu/suchenek/CSC311/Traversal2.jpg
Definition of binary search tree:
http://csc.csudh.edu/suchenek/CSC311/Def_BS_tree.txt
Playing
with BS Trees:
http://nova.umuc.edu/~jarc/idsv/lesson4.html
http://www.ibr.cs.tu-bs.de/courses/ss98/audii/applets/BST/BST-Example.html
Here is an example of deletemin() followed by delete(20) from a binary search tree:
http://csc.csudh.edu/suchenek/CSC311/BST_delete.pdf
BST_sort: the same as PQ_sort, except that the second phase (a sequence
of removes) has been replaced with in-order traversal of the BS tree
constructed in the first phase.
Related topic: QuickSort
(an emulation of BS-tree sort):
Simple
Split:
private static int
Split(int[] L, int lo, int hi)
//Uses
the
occupant
x
at index lo in array L as pivot,
//sends
all
elements
<
x to the begining of the range (lo, hi), and
//all
elements
>=x
to
the end of that range
{
int splitPoint = lo;
int x = L[splitPoint];
for (int i = lo+1; i <= hi; i++)
{
if
(Comp(L[i],
x))
//need
to move L[i] before split point
{
L[splitPoint]
=
L[i];
cnt2.incr();
splitPoint++;
L[i]
=
L[splitPoint];
cnt2.incr();
}
}
L[splitPoint] = x;
cnt2.incr();
return splitPoint;
}
Demo Split:
Array size = 20; max
no. of inversions = 190
Array:
500 400 621 229
702 40 243 312 247 46 711 241 637 898 24 15 872
595 182 635
95 inversions
Start Split: x = 500
400 621 229 702 40 243 312 247 46 711 241 637 898
24 15 872 595 182 635
400
621
229
702
40
243 312 247 46 711 241 637 898
24 15 872 595 182 635
400
229 621 702 40 243 312 247 46 711
241 637 898 24 15 872 595 182 635
400 229
40 702 621 243 312 247 46 711 241 637
898 24 15 872 595 182 635
400 229 40
243 621 702 312 247 46 711 241 637
898 24 15 872 595 182 635
400 229 40 243
312 702 621 247 46 711 241 637 898
24 15 872 595 182 635
400 229 40 243
312 247 621 702 46 711 241 637 898
24 15 872 595 182 635
400 229 40 243
312 247 46 702 621 711 241 637 898
24 15 872 595 182 635
400 229 40 243
312 247 46 241 621 711 702 637 898
24 15 872 595 182 635
400 229 40 243
312 247 46 241 24 711 702 637 898
621 15 872 595 182 635
400 229 40 243
312 247 46 241 24 15 702 637
898 621 711 872 595 182 635
400 229 40 243
312 247 46 241 24 15 182 637
898 621 711 872 595 702 635
End Split
400 229 40 243
312 247 46 241 24 15 182 500 637 898 621 711 872 595
702 635
56 inversions
splitPoint = 11
Here is a link to samle runs of several sorting algorithms presented in
forms of folk dances from
Central Europe:
http://www.youtube.com/user/AlgoRythmics
An example of a balanced
binary
search tree:

Here is a visualization of a BST that may
help you to se a BST on the picture above:

http://orion.lcg.ufrj.br/Dr.Dobbs/books/book3/109_a.gif
Here it is:

Examples of extended trees with 5 (internal) nodes:

http://orion.lcg.ufrj.br/Dr.Dobbs/books/book1/427_a.gif
Examples of extended
trees with 10 (internal) nodes:
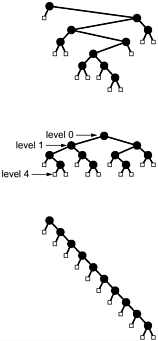
http://flylib.com/books/3/55/1/html/2/images/05fig23.gif

Exercises on external and internal path lengths:
http://csc.csudh.edu/suchenek/CSC311/Slides/IPL_exercise.jpg
http://csc.csudh.edu/suchenek/CSC311/Slides/EPL_exercise.jpg
http://csc.csudh.edu/suchenek/CSC311/Slides/IPL_EPL_exercise.jpg
Notes on external and internal path lengths:
http://csc.csudh.edu/suchenek/CSC311/External_internal_path.pdf
Computations
of the minimum, average, and maximum EPL and IPL, with applications
to best, average, and worst performance of BS Trees:
Best case:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Min_ipl_epl.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Min_ipl_epl.pdf
Average case:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Avg_ipl_epl.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Avg_ipl_epl.pdf
Worst case:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Max_ipl_epl.nb
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Max_ipl_epl.pdf
The rest of this section is optional.
Here is a
graph of a ratio of the number all permutations on n elements to the
number of binary search trees with n elements:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Ratio_perms_to_BSTrees.pdf
Here is a
graph of a ratio of the number all binary search trees with n
elements to the number of the tallest binary search trees with n
elements:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/BST_worst_fraction.pdf
Here are
Mathematica calculations of the number of the shortest binary search
trees of height H:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Explicit_number_of_best_BST.pdf
and the graph
of that number in function of H:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Explicit_number_of_best_BST_graph.pdf
and the same
graph with the number of tallest binary search trees superimposed:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Explicit_number_of_best_BST_v_worst.pdf
Here
is the ration of the number of n-permutations that result in the best
(shortest) BSTs to the number of n-permutations that result in the
worst (tallest/skinniest) BSTs:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Ratio_of_best_to_worst_BST1.pdf
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Ratio_of_best_to_worst_BST2.pdf
Hashing and ADT TABLE
Link
to
slides:
http://csc.csudh.edu/suchenek/CSC311/Slides/Hash.pdf
It's a copyrighted
material, so the students in this class can read them but not to copy or distribute
them.
Von Misses probability argument:
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Probability_of_same_birthdays.pdf
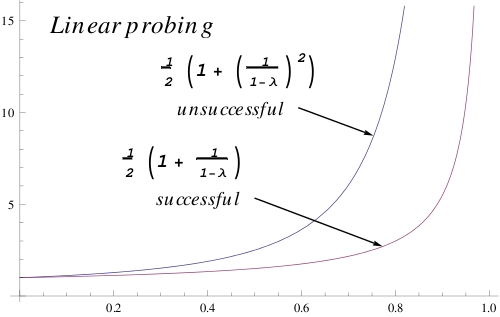
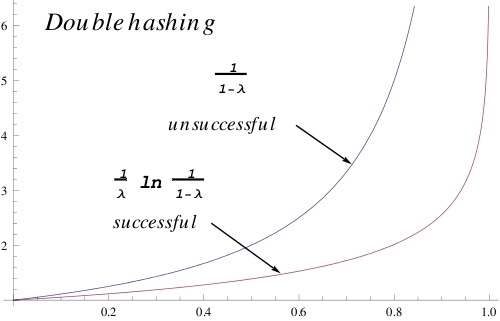
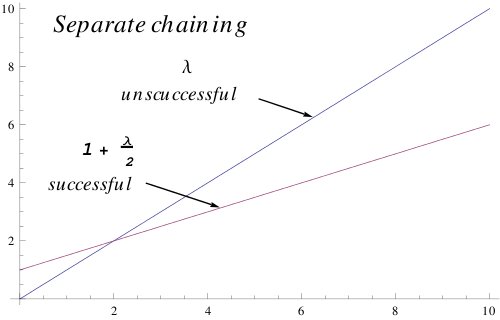
Notes on performance of hashing:
http://csc.csudh.edu/suchenek/CSC311/Hash_performance.pdf
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Hash_performance.pdf
http://csc.csudh.edu/suchenek/CSC311/Mathematica/Hash_performance.nb
That's all, folks!

|
|